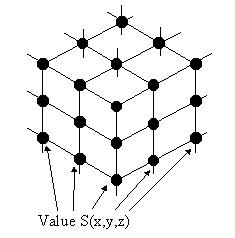
Suppose that a volume model of a room is given. The volume is divided into cells, and the temparature values of the room are given at each vertex.

|
Results of 3D numerical simulations or medical measurements
are usually preserved in volume data structures,
consists of cells dividing the 3D domain.
Scalar values obtained from the simulations or measurements
are usually assigned to all vertices of the cells.
The set of values at the vertices can be regarded as a
scalar field in the volume damain.
Suppose that a volume model of a room is given. The volume is divided into cells, and the temparature values of the room are given at each vertex. |
|
Often we are interested in the representation of surfaces
consist of points that have equal values.
Isosurface is a set of polygons, which interpolate the point
that have the equal value C=S(x,y,z).
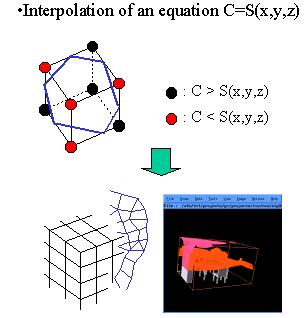
Suppose that we are thinking of where to put an heater in the room. If you want to keep the room at 26 degrees centigrade, You should want to see which area is 26 degrees. You can see such an area by generating an isosurface regarding the constant value C as 26. In a typical implementation, vertices of an isosurface is assigned on edges of cells by the linear interpolation between values of two vertices of the edges. A polygon inside a cell is generated by connecting the vertices. Isosurface is generated by applying the process to all cells in a volume. |
|
|
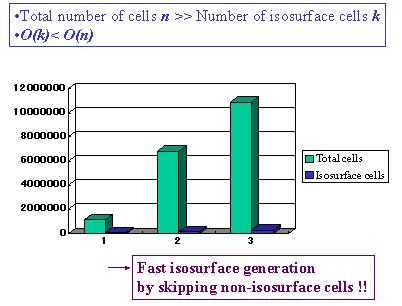
Isosurface generation is costly,
if you visit all the millions of cells.
In our observation, usually the number of isosurface cells
are much less than the total number of cells in a volume.
Here is our motivation. Isosurface generation can be dramatically acceralated if we can skip many of non-isosurface cells. |
| Isosurface cells are adjacent each other. If one isosurface cell is found, other isosurface cells can be found by visiting adjacent isosurface cells in order. Our solution is the fast isosurface cell extraction and recursive adjacent isosurface cell search. It avoids to visit other most cells, so the isosurface generation process can be dramatically acceralated. |
 |
|
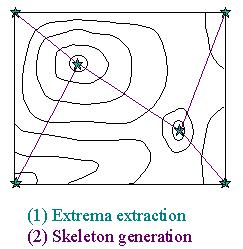
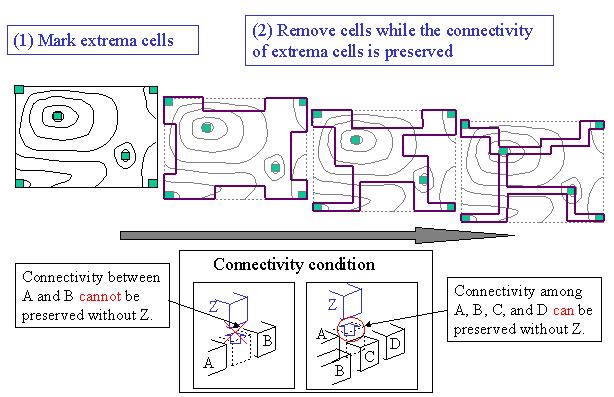
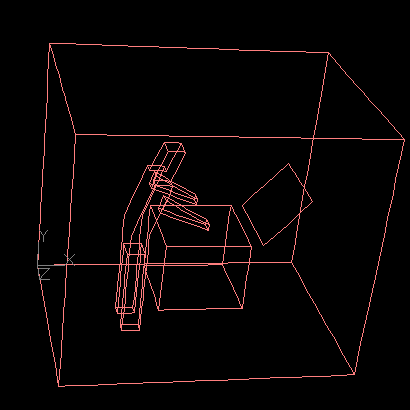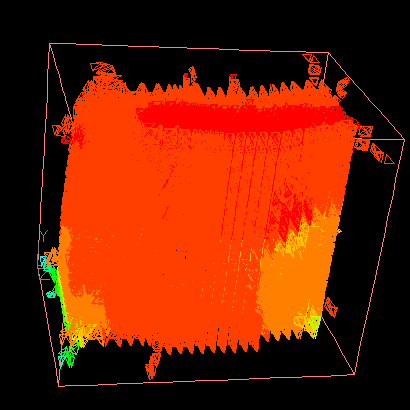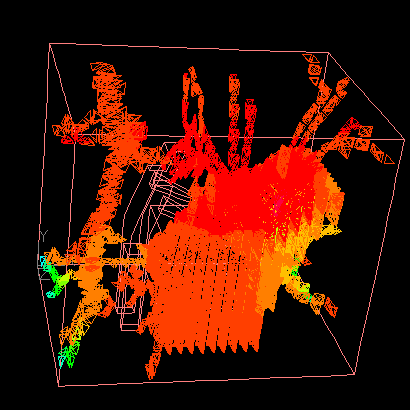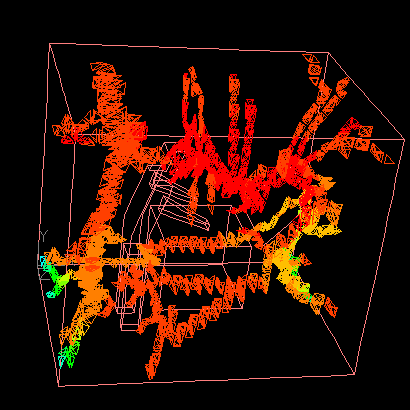
Now we propose the extrema skeleton, that is a set of cells
connecting the extrema (=local minimum or local maximum)
points of a scalar field inside the volume domain.
To form an extrema skeleton, our implementation first visits the vertices of a volume, and extracts the extrema vertices. Then it constructs the skeleton consists of cells. The process takes a couple of seconds, but it is just a pre-processing, and needs only one time. |
|
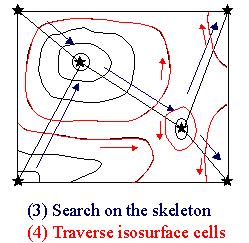
Given a constant value C, our implementation first searches
for isosurface cells on the skeleton.
At least one isosurface cell in every parts of an isosurface
is necessarily found, and their adjacent isosurface cells
are recursively visited in order.
An isosurface is completely generated when the visit is
terminated, while other most cells are not visited.
If you want many isosurfaces with varying the constant value C, the method is especially useful, because you do not have to generate the skeleton any more. |
|
| We applied the volume thinning method to form an extrema skeleton. The method first marks cells adjacent to extrema vertices, and then removes many cells out of the process, while it preserves the connectivity between the marked cells. Finally an extrema skeleton that connects all the extreama vertices is formed. Isosurface cells of every isosurfaces can be always found from the skeleton. |
 |
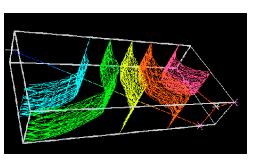
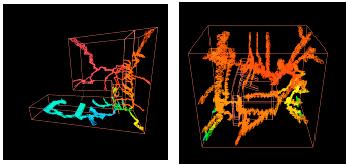
| The left image is a very simple example of an extrema skeleton and five isosurfaces. The right image is two examples of more complecated extrema skeletons. |
|
|
The following image shows an example of the volume thinning process. |
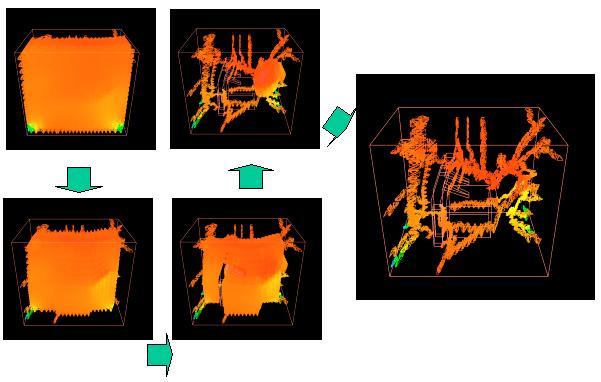
|
|
The animation shows an example of volume thinning process. |
|
|
The animation shows an example of iteractive isosurface generation process. |
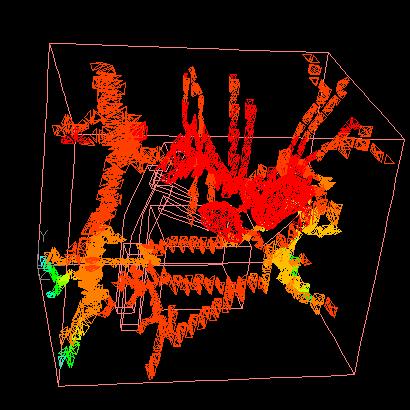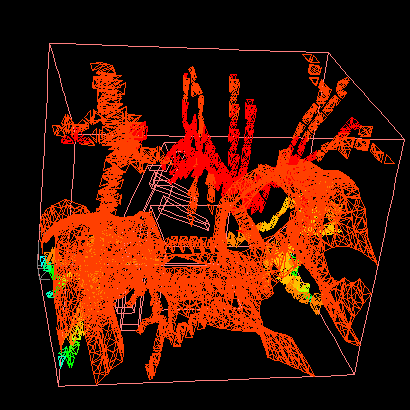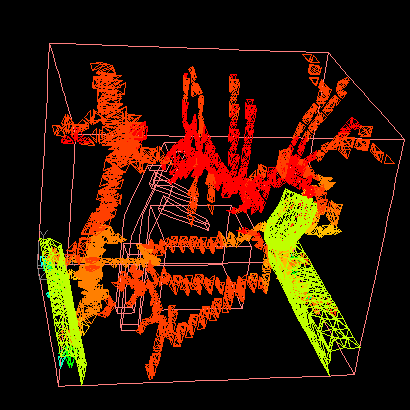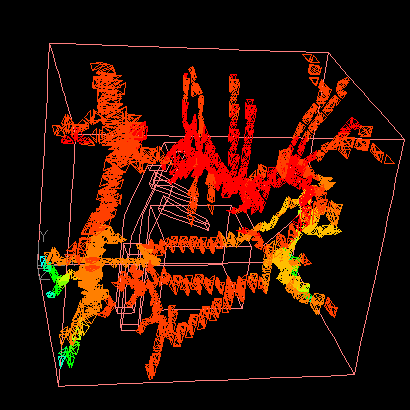
|
|
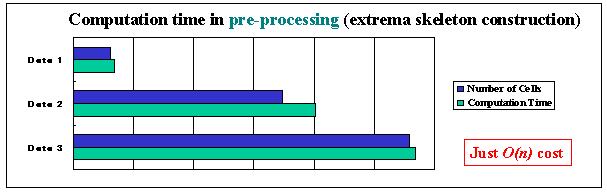
The following graph shows the number of cells in three volumes and computation times for constructing extrema skeletons for the three volumes. It denotes that the computation time is almost proportinal to the number of cells. It is natural because the extrema vertices extraction process visits each vertex once, and the volume thinning process visits each cell once. |
|
|
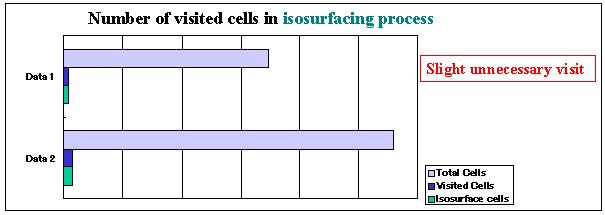
The following graph shows the total number of cells, visited cells to generate isosurfaces in our method, and actual isosurface cells, in the three volumes. It denotes that our method skips most of non-isosurface cells, therefore it archived to reduce the computational time dramatically. |
|
|
Some other researchers have also presented the similar approach that skip most of non-isosurface cells, and they have also archived the acceralation of isusorface generation process. It seems that differnce of the cost of isosurface generation process is slight between their methods. Remark the cost of pre-processing. Most of their approaches requires more than O(n) computation time, while our implementation requires just O(n) computation time for the pre-processings. It is a main advantage of our method. |
Itoh T. et al., Isosurface Generation by Using Extrema Graphs, IEEE Visualization '94 Proceedings, pp. 77-83, 1994.
Itoh T. et al., Automatic Isosurface Propagation by Using an Extrema Graph and Sorted Boundary Cell Lists, IEEE Transactions on Visualization and Computer Graphics, Vol. 1, No. 4, pp. 319-327, 1995.
Itoh T. et al., Volume Thinning for Automatic Isosurface Propagation, IEEE Visualization '96 Proceedings, pp. 303-310, 1996.
Itoh T. el al. Fast Isusurface Generation Using an Extrema Skeleton
and Cell-Edge-Centered Propagation,
IEEE Transactions on Visualization and Computer Graphics,
Vol. 7, No. 1, pp. 32-46, 2001.