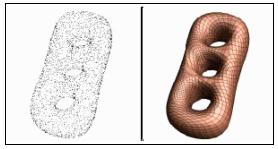
Surface reconstruction is a technique for converting fine polygonal surfaces or unorganized points into fewer number of parametric surface patches. For example, range scanner extracts the shape of objects as a set of unorganized points. Surface reconstruction techniques generate a set of parametric surface patches represent the same shape as the object.

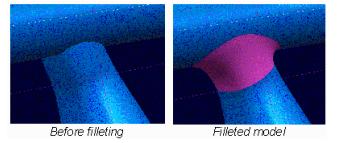
We have applied the surface reconstruction technique to the automated fillet modeling system. Our implementation first generate a smooth triangular mesh connecting two parts, and then converts the mesh into parametric surface patches.

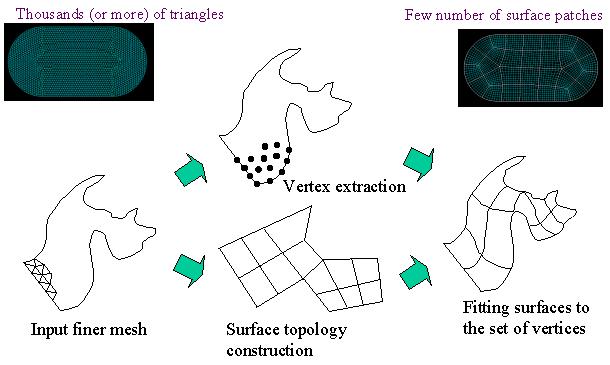
To convert the fine triangular mesh into coarse surface patches, our implementation first constructs the topology of quadrilateral patches. Then, it regards the vertices of the triangular mesh as a set of unorganized points, and fits the quadrilateral patches into the set of points by using the least-square-based interpolation.

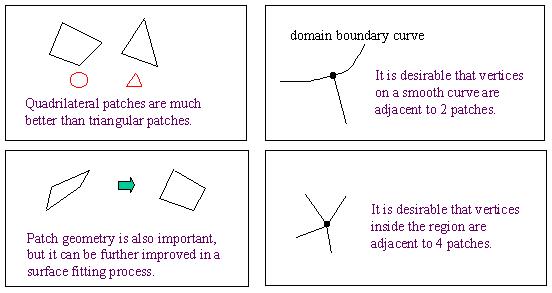
We experimentally found that the smoothness and continuity of surface patches strongly depens on their topology. The following is the requirements for the topology we found in our try-and-error. All four requirements are important, but we think that the topology along the domain boundary is especially critical in the view of the quality of surfaces.

These requirements are very similar to those for meshes used in finite element analyses. We learned the advancing front method, which generates high quality meshes for finite element analyses, so that we develop a method for generating a surface topology that satisfies the above requirements. The advancing front method generates elements starting from the domain boundary, toward the interior of the domain. Elements generated by the advancing front method are well-aligned along the domain boundary, as if they form several layers toward the interior of the domain. It is well-known that meshes generated by the advancing front method is usually good at their topology.

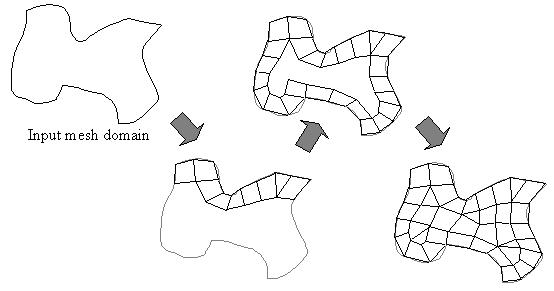
To generate the topology of surface patches like those of meshes generated by the advancing front method, our implementation first generates several belt-like subregions along the domain boundary, by clustering triangular elements. It first generates a set of one-element-width layers, and constructs a graph of the layers. Then it merges many of the layers to form several subregions. The process corresponds to the simplification of the layer graph. The following is an example of subregion generation. The implementation generates only two subregions from about 50 of one-element-width layers, and generates quadrilateral patches by cutting the subregions.

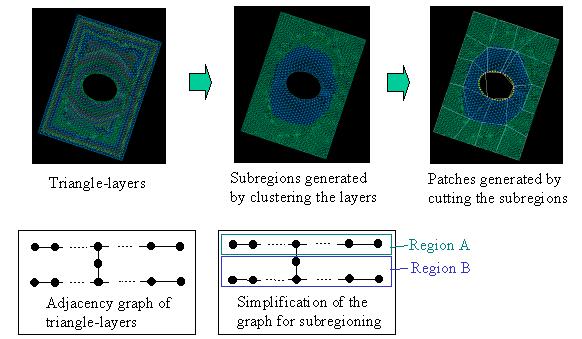
The following animation shows the generation of belt-like subregions, surface patch generation inside each subregion, and surface patch fitting into the input triangular mesh. Finally a set of smooth and continuous surface patches are constructed.

These are examples of surface patchs generated by the method. The results do not entitely satisfies the requirements, but they topologically look well.

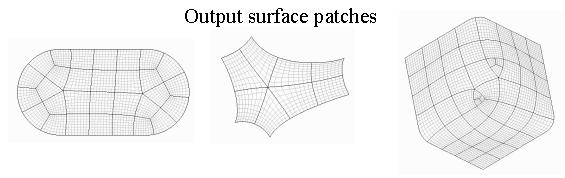
Our study is just experimental, so we should evaluate about the method more. The smoothness and continuity of surface patches should be numerically compared with the patches constructed by the diffrent way. Besides, we should theorically think why the requirements are necessary. They will be our future works.


Related publications:

Itoh T., et al., Rough Quadrilateralation of Triangular Meshes via Belt-like Subregioning for Surface Reconstruction, IBM Research, TRL Research Report, RT0354, 2000.