In some numerical analyses, such as automobile crash simulation, quadrilateral meshes are preferred to triangular meshes in the view of the accuracy and convergency of the analyses solutions.

In many cases, directionality of mesh elements is important. It is often desirable that elements are well-aligned along the flow of phenomena. It is also often desirable that elements are well-aligned along the domain boundary. To satisfy these various requirements about the directionality of meshes, we began to the development of quadrilateral mesh generation method under the new concept, that flexibly controls the directionality according to a vector field that represents the user-desired directionality.

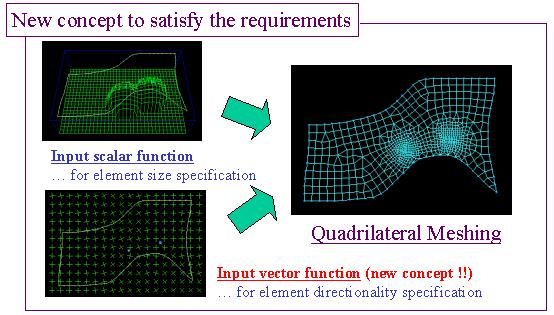
By the way, we have developed the bubble mesh method, for triangular mesh generation. The method properly locates vertices of a triangular mesh, and the mesh is generated by connecting the vertices. In this method we assume a particle model that has attractive and repulsive forces, like the van del Waals model. By solving a motion equation of particles, their location is fixed. The sizes of triangular elements are flexibly controlled, given a scalar field that represents the distribution of user-desired element sizes.

We thought that another particle model is more suitable to quadrilateral meshing, but what is that ? We tried to develop the another "square" particle model instead of the circular particle model. Given scalar and vector functions that represent user-desired element sizes and directionality, our implementation packs the square particles, by solving the motion equation of square particles. Finally the particles are orthogonally packed inside the domain, well-aligned along the given vector field.

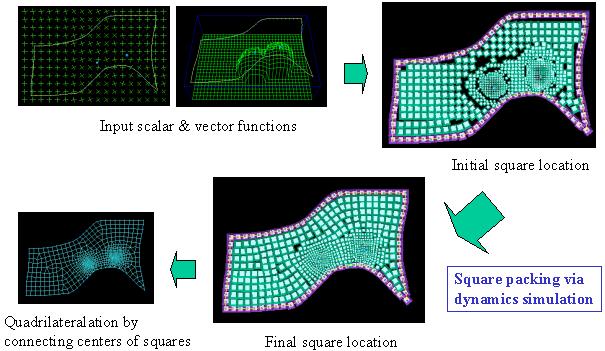
The following image shows the difference of potential field of forces of a particle between a circle and a square. We implemented the potential field of a square as a sum of five functions, that have local-maximum values at the center and four corners of the square particle.

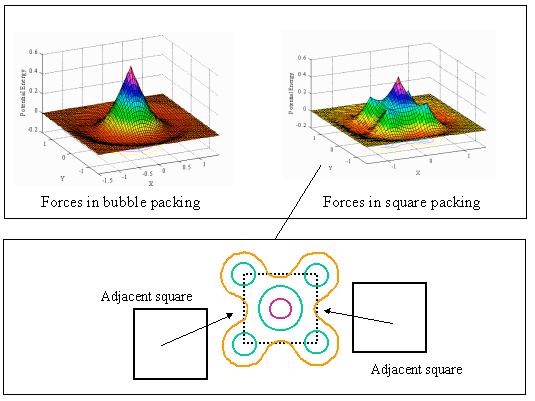
The follwoing animation is an example of the packing of square particles.

We also have to develop a method for connecting the vertices to form quadrilateral elements. However, it is not easy to directly form quadrilateral elements from the unorganized vertices. Therefore we tried to develop the two-pass algorithm, that first generates a triangular mesh by connecting the vertices, and then erase some of connection to convert the triangular elements into quadrilateral elements. In the other researcher's paper, it is demonstrated that the two-pass solution is not only easy to implement but also experimentally faster.

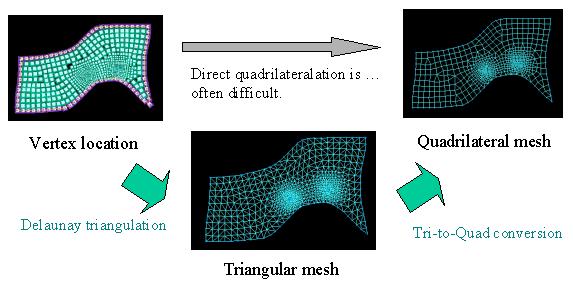
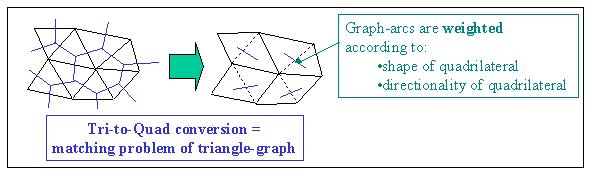
The conversion of triangular meshes into quadrilateral meshes is a kind of matching problem of a graph weighted by the shape and directionality of quadrilateral elements. We implemented the O(n log n) algorithm that evaluates all possible quadrilaterals according to their shapes and directions, and then converts the pairs of triangles in the order of the evaluation values.

The feature of our approach is the generation of well-shaped, well-graded, and well-directionized quadrilateral meshes. Especially, flexible control of mesh directionality seem the most unique feature of the method.


Related publications:

Shimada K., et al., Quadrilateral Meshing with Directionality Control through the Packing of Square Cells, 7th International Meshing Roundtable, pp. 61-76, 1998.

Itoh T., et al., Automated Conversion of 2D Triangular Mesh into Quadrilateral Mesh with Directionality Control, 7th International Meshing Roundtable, pp. 77-86, 1998.

Itoh T., A Study on Automated Quadrilateral Mesh Generation Methods, JSST Journal, Vol. 18, No. 2, pp. 19-25, 1999 (written in Japanese).

Itoh T., et al., Automatic Conversion of Triangular Meshes into Quadrilateral Meshes with Directionality, International Journal for CAD/CAM, Vol. 1, No. 2, pp. 20-38, 2001.